
목차
기본치수 없이 쓰이는 위치공차
CASE 1: 형상에 수직 한 데이텀인 경우

바닥면(C)에 수직한 상태를 유지하면서 생겨라!
CASE 2: A형상의 축에 B형상의 축을 맞추는 경우

한쪽 축을 다른쪽 축에 맞춰라!
* 현실에서 두 축이 완벽히 일치할 수가 없음.
왼쪽 축은 데이텀 A (rlwns)
오른쪽 축은 검사대상
오른쪽 축을 검사했을 때 왼쪽축 중심을 참고하여 생긴 공차역에 들어오면 합격

CASE 3: A형상의 중심평면에 B형상의 중심평면을 맞추는 경우

여기서 데이텀 A: 마주보는 두 면을 시뮬레이팅해서 찾아낸 중심평면

위치공차를 막 갖다 붙여 도면 해석이 안 되는 경우 / 예시
위치공차는 반드시 FOS에만 붙일 수 있음
위치공차 → 이 형상의 센터가 공차역 안에 들어오도록 하자
첫 번째 예제
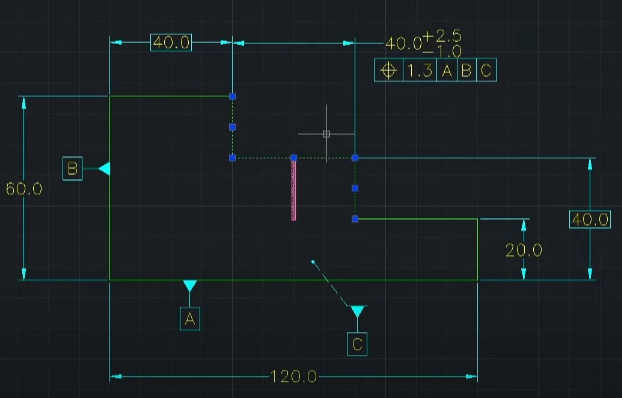
- 위 같은 경우 기하공차 부분이 FOS가 아님.
- 각 면 모두 오른쪽을 바라보는 형태기 때문에 공차역을 정의할 수 없기 때문에 해석이 안 되는 케이스임
두 번째 예제
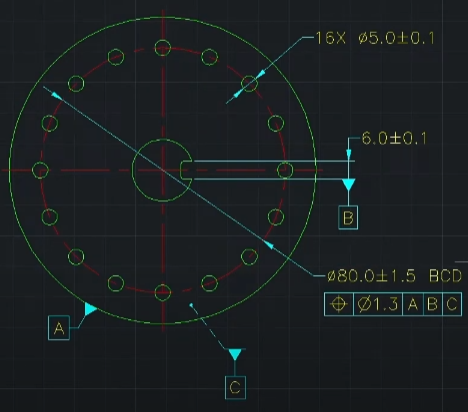
- 위 같은 경우 기하공차의 위치가 잘못됨.
- FOS는 맞으나 컨트롤하고자 하는 형상은 16X Ø5.0+-0.1 부분이기 때문에 해당 공차에 기하공차를 넣어야 함.
세 번째 예제
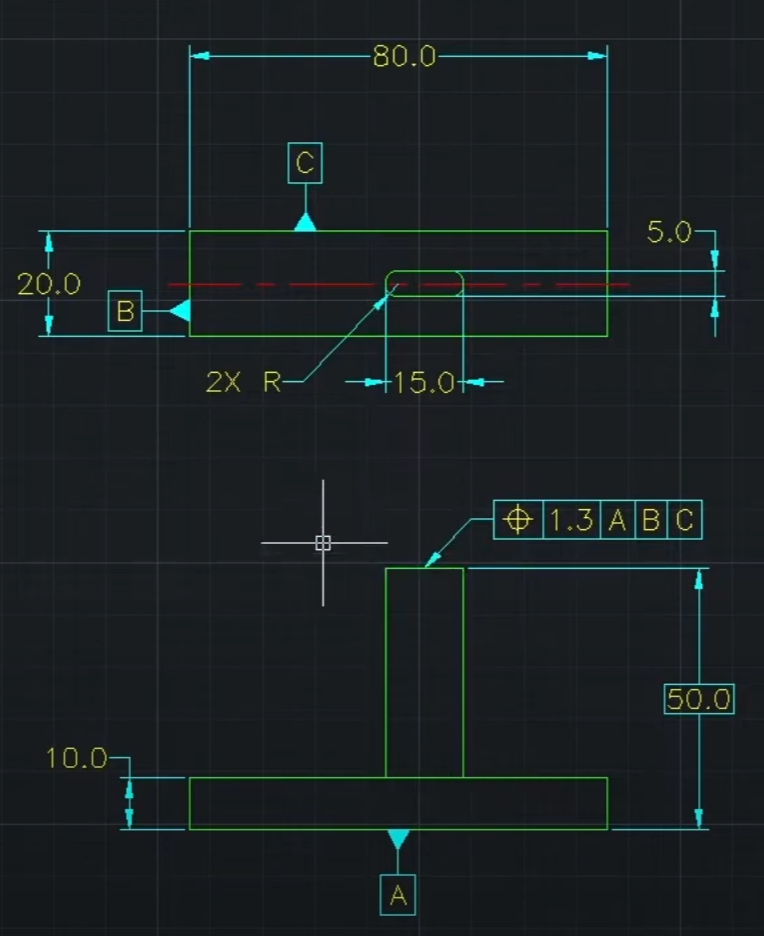
- FOS가 아니기 때문에 해석이 안 되는 케이스임
네 번째 예제
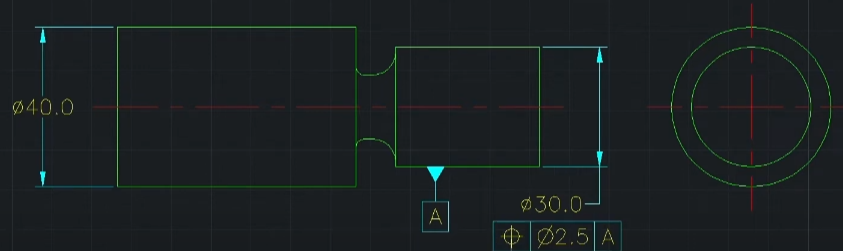
- 데이텀 A의 위치가 오른쪽에 있으면 안됨
- 데이텀 A는 왼쪽 축에 위치해야 하며 오른쪽 축을 검사했을 때 왼쪽 축 중심을 참고하여 생긴 공차역에 들어오면 합격함.
다섯 번째 예제
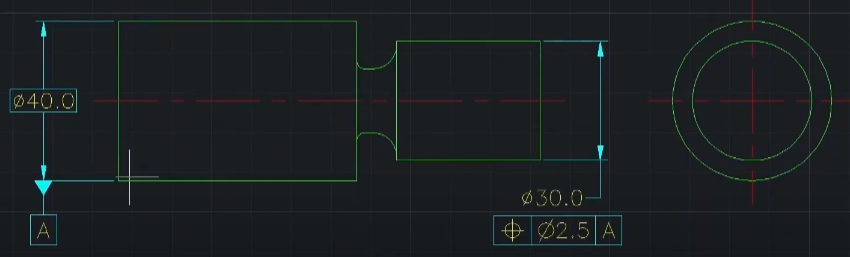
- 다 좋은데 왼쪽에 기본치수를 넣어 틀린 케이스
완벽한 예제
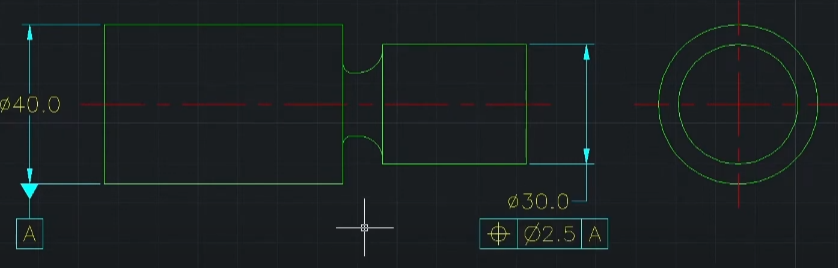
동심도공차와 대칭도공차

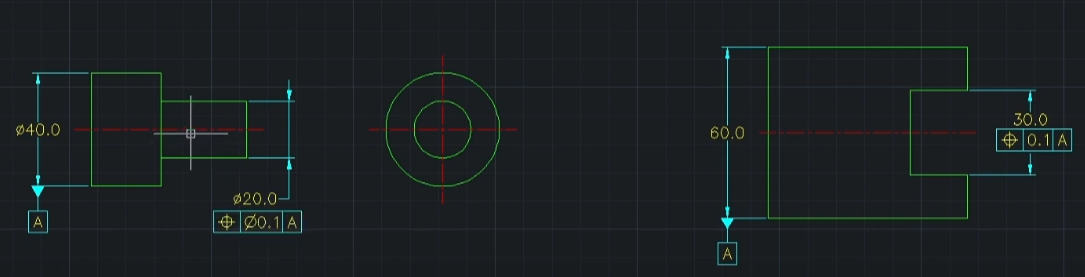

- 표면이 쭈글쭈글하다고 축과 평면도 그러냐? No
- 축 = 곧다
- 중심평면 = 평평하다
- 두 전제는 깔려있어야 한다.
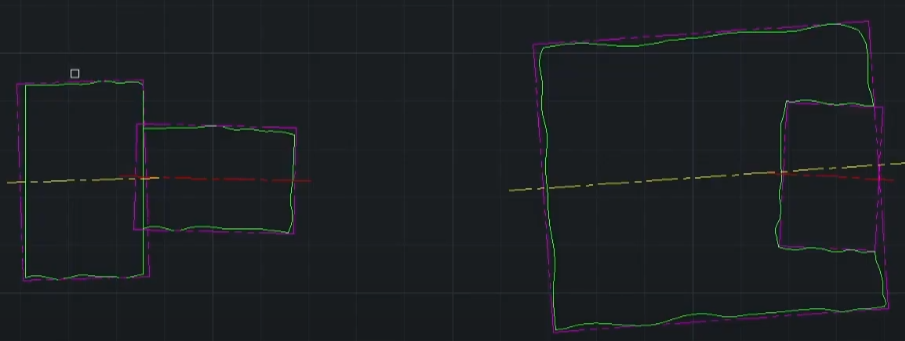
- 윗면 아랫면에 딱 붙으면서 완벽히 평행을 이루고 있는 평면이 점점 다가오면서 맞물리는 순간 더 이상 좁혀지지 못하는 경계선
- AME (Actual Mating Envelop)
- 멀리 떨어진 두 평면이 거리를 좁히면서 제품의 각 면의 돌출 된 세 점에 닿는 외관면 (마젠타 색)
- 형상의 축 = AME의 축
즉, 위치도는 "축 VS 축 / 중심평면 VS 중심평면"을 본다.
또한 축은 언제나 곧고 중심평면은 언제나 평평하다
그렇기 때문에 위치도는 언제나 축(Axis)과 중심평면(Center Plane)의 개념을 사용하여 해석함
대신 동심도나 대칭도는 축이나 중심평면 대신 다른 개념을 사용한다. <- 이 것이 가장 결정적인 차이점
동심도와 대칭도는 축이나 중심평면이 아니라 Median Point를 사용함
Median Point = 중심
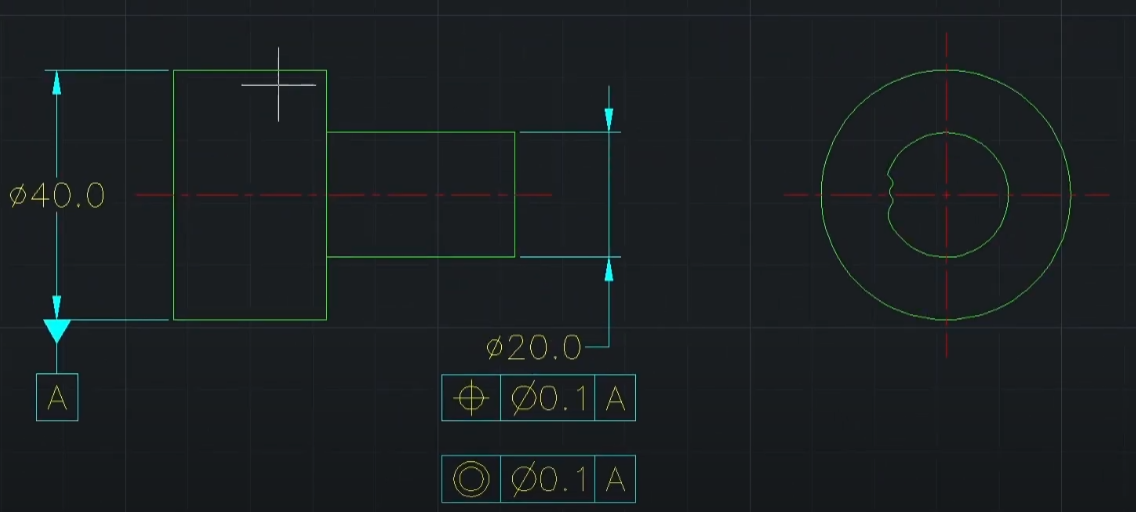
- 모든 점의 모든 Median Point를 다 구해야 함.
- 한 점이라도 공차역 밖으로 나가면 불합격임
- 동심도: 축 VS MP
- 대칭도: 중심평면 VS MP
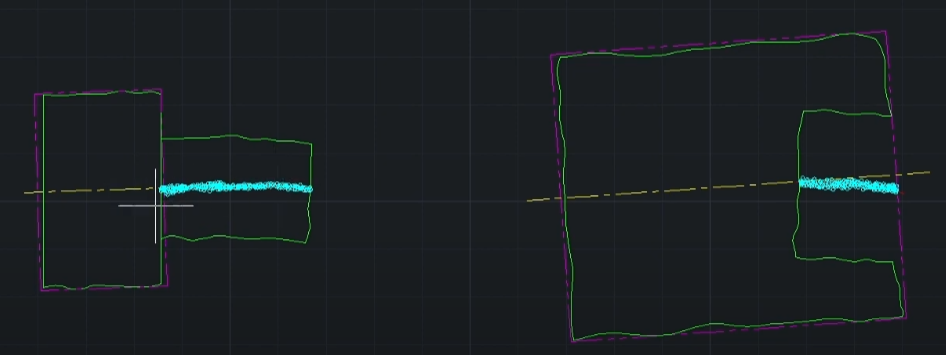
- 위치도일 경우에는 AME 영향을 못 미쳐 합격함.
- 하지만 동심도일 경우에는 축VS축이 아니라 축VSMP기 때문에 불합격됨.
즉, 위치도보다 동심도가 기준이 빡세다.
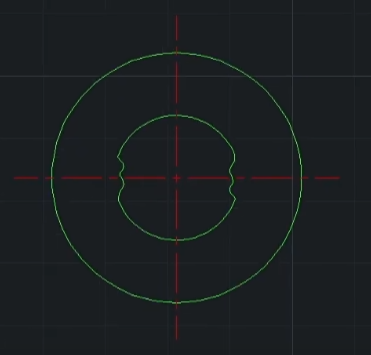
- 위와 같이 찌그러짐도 평행하다면 MP가 중앙으로 잡혀 동심도 요건 만족가능함.
동심도와 대칭도는 M L과 같은 모디파이어 사용 불가능함.
- 주의할 점: ISO에서는 위치공차도 Median Point를 통해 검사함.

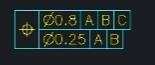
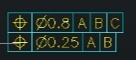
위치공차 두 줄 짜리는?
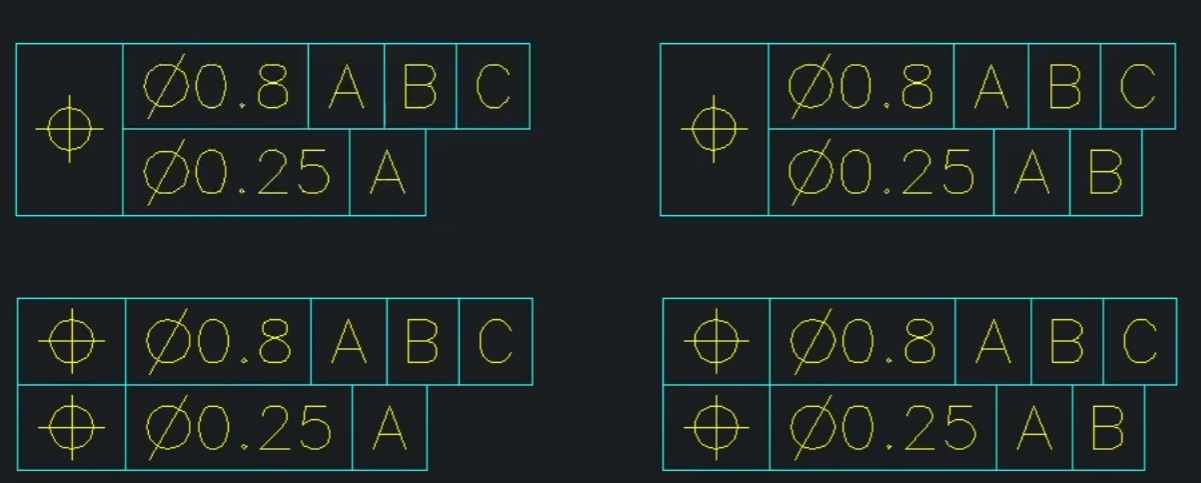
- 패턴의 로케이션을 스케일할 때 쓰인다.
(패턴: 형상이 반복적으로 일어나는 것)
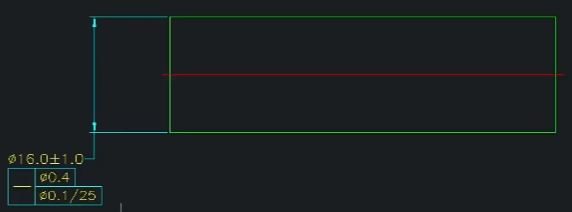
- 윗줄은 전체적인 요건 (공차역이 큼)
- 아랫줄은 (디테일한, 세심한) 다듬는 요건 (공차역이 작음)
예제)
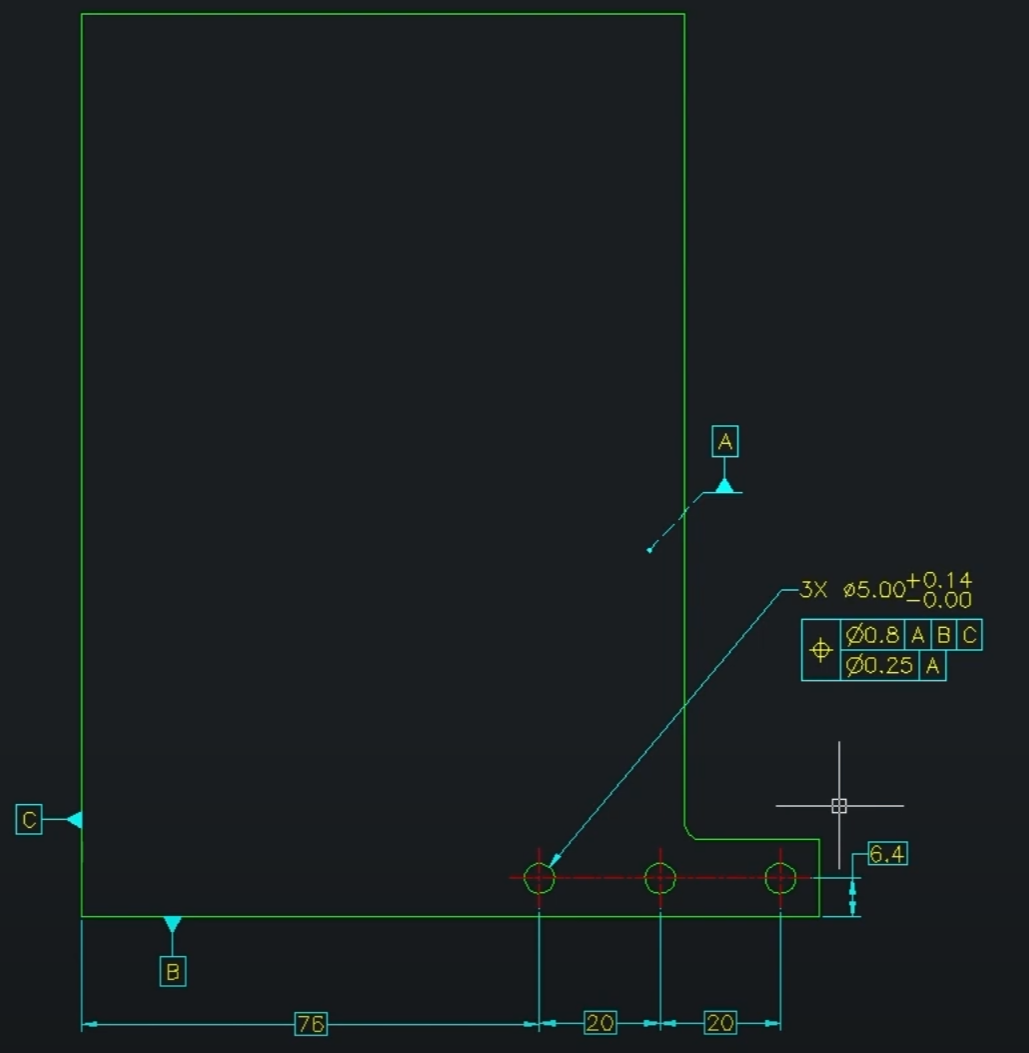
패턴: 5파이짜리 원 3개 (같은 형상 반복)
패턴외부치수: 76, 6.4
패턴내부치수: 20 (패턴 엘리멘트 사이의 관계를 규정짓는 것)
이후, 패턴 해석
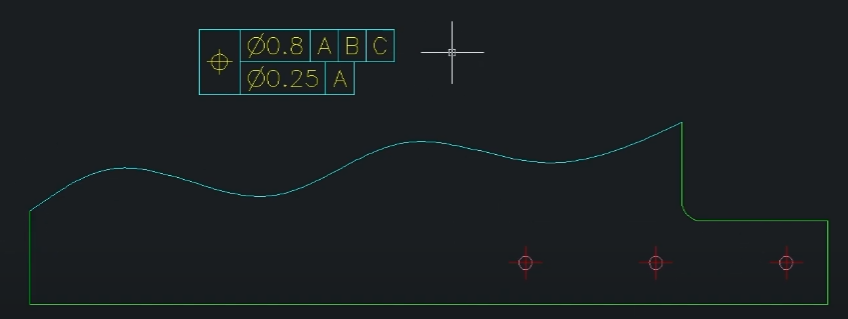
윗줄을 해석할 때,
1. 공간 상에 고정되어있는 공차역을 도출한다.
2. 패턴 내부 및 외부 치수를 모두 사용하여 공차역을 도출한다.
아랫줄을 해석할 때,
1. 공차역이 공간상에 고정되어있지 않다.
2. 패턴 내부 치수만 사용하여 공차역을 도출한다.
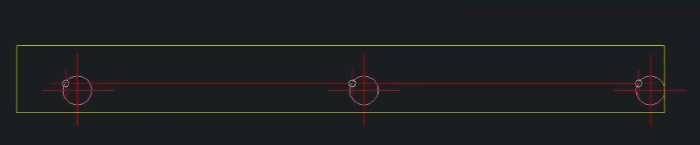
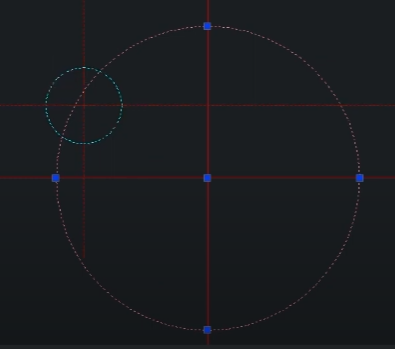
첫번째 공차역과 두번째 공차역의 교집합 안에 들어오면 합격 아니면 불합격
두번째 줄의 위치도가 데이텀A를 참조하고 있으므로 공차역은 데이텀 A에 수직함을 유지하면서 도출된다.
'설계' 카테고리의 다른 글
| ⑦ 도면해독능력 키우기 (MMB: Maximum Materical Boundary) (1) | 2024.02.12 |
|---|---|
| ⑥ 도면해독능력 키우기 (모양공차) (0) | 2024.02.12 |
| ④ 도면해독능력 키우기 (데이텀) (0) | 2024.02.12 |
| ③ 도면해독능력 키우기 (기하공차) (0) | 2024.02.12 |
| ② 도면해독능력 키우기 (공차) (0) | 2024.02.12 |



